Integrity
What do we prove?
LuminAIR’s primary goal is to cryptographically demonstrate that a computational graph has been executed correctly. This proof allows verifiers to validate the integrity of the computation using significantly fewer resources than re-executing the graph.
The underlying technology enabling this is STARKs (Scalable Transparent Arguments of Knowledge), which ensures computational integrity through a transparent, scalable, and post-quantum secure proof system.
How STARKs Work?
How STARKs Work?
STARKs are based on transforming computations into algebraic representations, enabling the creation of cryptographic proofs of correctness. Here’s an overview of how they work:
- Arithmetization
- The first step in STARKs is arithmetization, where a computational problem is converted into an algebraic form. This involves expressing the computation as a sequence of operations over finite fields.
- The computation is represented as an Algebraic Intermediate Representation (AIR), which defines constraints as polynomials over trace cells. These constraints ensure that the computation satisfies certain properties.
- Execution Trace
- During execution, the state of the computation at each step is recorded in an algebraic execution trace. This trace consists of tuples of values (or “registers”) from a finite field.
- The trace captures the evolution of the computation, step by step, and serves as the foundation for constructing proofs.
- Low-Degree Polynomials
- The prover interpolates the execution trace into low-degree polynomials. These polynomials encode the entire computation in a compact mathematical form.
- The AIR constraints are then expressed as operations on these polynomials, ensuring that only valid computations produce low-degree polynomials.
- Proof Generation
Using techniques like FRI, the prover generates a cryptographic proof that certifies:
- The algebraic execution trace satisfies all AIR constraints.
- The polynomials derived from the trace are indeed low-degree. This proof is succinct, meaning it is much smaller than the original computation.
- Verification
- The verifier checks the proof probabilistically by sampling specific points on the polynomials. If these points satisfy the constraints, it is overwhelmingly likely that the entire computation was executed correctly.
- This process requires far fewer resources than re-executing the original computation, making STARKs highly efficient for verification.
Using STARKs to Prove Computational Graphs
Mapping Computational Graph Nodes to AIR Components
In LuminAIR, computational graphs are transformed into AIR constraints and executed to generate an algebraic execution trace.
Each operator corresponds to a distinct AIR component, which has its own set of local constraints. These constraints ensure that each operation in the graph is executed correctly.
Ensuring Data Flow Integrity Between Nodes
While each AIR component verifies its local operation, it is equally important to ensure proper data flow between nodes in the computational graph. Specifically, the output of one node must match the input of another node.
This consistency is enforced using the LogUp lookup argument protocol, which establishes a system of relations between tensor values.
Output Yields (Positive Multiplicity)
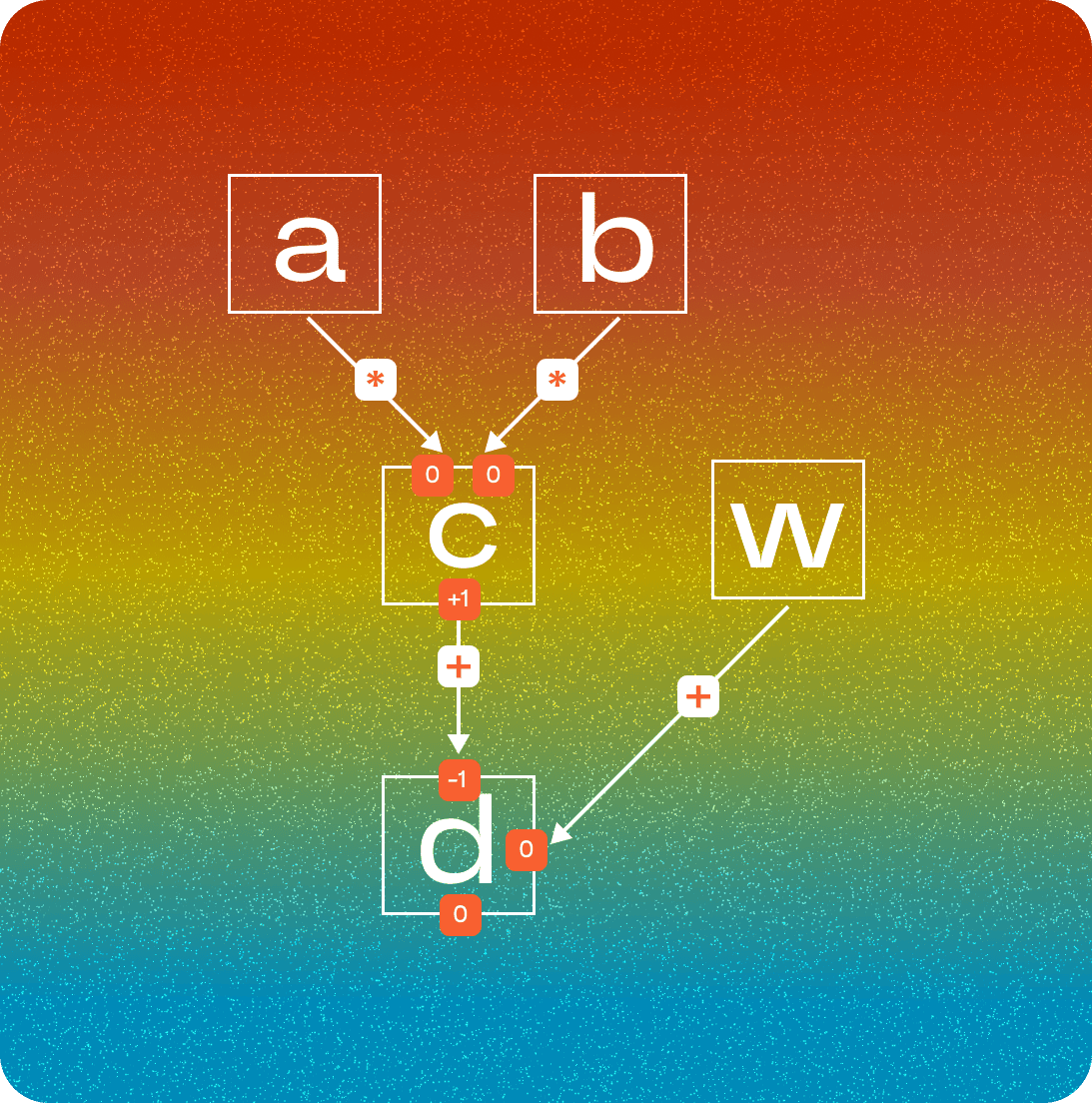
- When a node produces an output that will be consumed by other nodes, its multiplicity equals the number of consumers.
- This indicates that the value is “yielded” for use elsewhere in the graph.
Input Consumes (Negative Multiplicity)
- When a node receives an input from another node, its multiplicity is
-1. - This signifies that the value is “consumed” by the operation.
Special Cases (Zero Multiplicity)
- Graph Inputs (Initializers): Tensors that serve as initial inputs to the graph have zero multiplicity because they are not consumed by any prior operation.
- Graph Outputs (Final Results): Tensors that represent final outputs of the graph also have zero multiplicity since they are not yielded to subsequent operations.